希尔排序简单应用

简单插入排序缺陷

我们看简单的插入排序可能存在的问题.

数组 arr = {2,3,4,5,6,1} 这时需要插入的数 1(最小), 这样的过程是：

{2,3,4,5,6,6}

{2,3,4,5,5,6}

{2,3,4,4,5,6}

{2,3,3,4,5,6}

{2,2,3,4,5,6}

{1,2,3,4,5,6}

结论：当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响。

希尔排序介绍

希尔排序是希尔（Donald Shell）于 1959 年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。

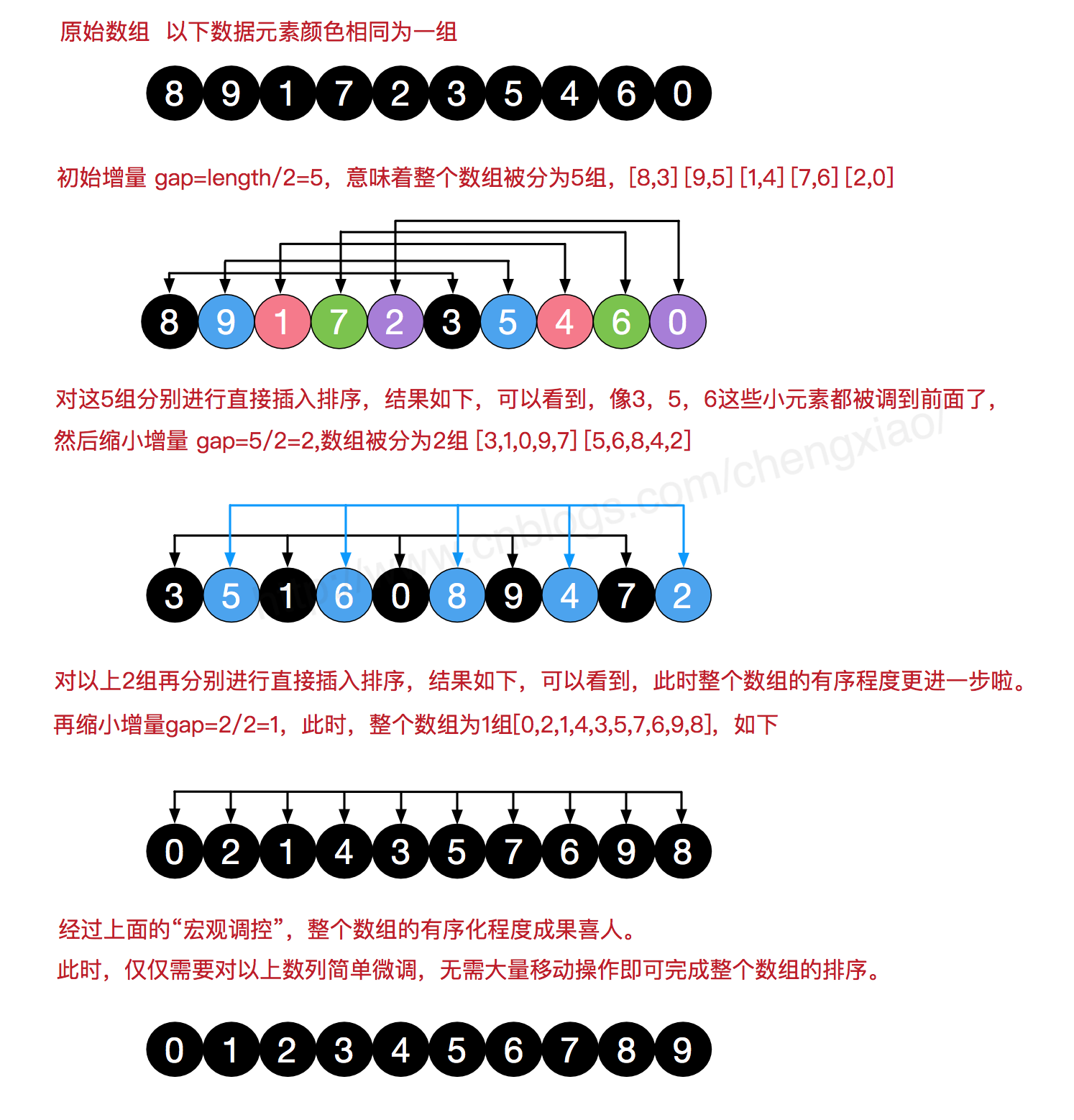
希尔排序基本思想

希尔排序的基本思想是：是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

代码实现

交换法

希尔排序时， 对有序序列在插入时采用交换法。

public class ShellSort1 {
    public static void main(String[] args) {
        int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
        System.out.println("排序前的数组为：" + Arrays.toString(arr));
        shellSort1(arr);
    }

    /**
     * 希尔排序-->交换法
     * 经测试，80000 随机数据排序用时 6s
     * @param arr
     */
    public static void shellSort1(int[] arr) {

        int temp = 0;
        int count = 0;
        //外循环：按【步长gap】匹配分组，哪些元素放在一组
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            //内循环：对每一组元素由后往前交换排序
            for (int i = gap; i < arr.length; i++) {
                // 遍历各组中所有的元素(共gap组), 步长gap
                for (int j = i - gap; j >= 0; j -= gap) {
                    // 如果当前元素大于加上步长后的那个元素，说明交换
                    if (arr[j] > arr[j + gap]) {
                        temp = arr[j];
                        arr[j] = arr[j + gap];
                        arr[j + gap] = temp;
                    }
                }
            }
            System.out.println("希尔排序第" + (++count) + "轮 =" + Arrays.toString(arr));
        }
    }
}

移动法

希尔排序时， 对有序序列在插入时采用移动法。

public class ShellSort2 {
    public static void main(String[] args) {
        int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
        System.out.println("排序前的数组为：" + Arrays.toString(arr));
        shellSort2(arr);
    }

    /**
     * 希尔排序优化-->移位法
     * 经测试，80000 随机数据排序用时 1s
     * @param arr
     */
    public static void shellSort2(int[] arr) {

        // 增量gap, 并逐步的缩小增量
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            // 从第gap个元素，逐个对其所在的组进行直接插入排序
            for (int i = gap; i < arr.length; i++) {
                int j = i;
                int temp = arr[j];
                if (arr[j] < arr[j - gap]) {
                    while (j - gap >= 0 && temp < arr[j - gap]) {
                        //移动
                        arr[j] = arr[j - gap];
                        j -= gap;
                    }
                    //当退出while后，就给temp找到插入的位置
                    arr[j] = temp;
                }

            }
        }
    }
}