递归简单案例：迷宫问题与八皇后问题

本文最后更新于：2 年前

关于递归（Recursion）

调递归就是方法自己调用自己，每次调用时传入不同的变量。递归有助于编程者解决复杂的问题，同时可以让代码变得简洁。

  • 8皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题（ google 编程大赛）
  • 各种算法中也会使用到递归，比如快排，归并排序，二分查找，分治算法等
  • 用栈解决的问题——–>用递归代码比较简洁

递归调用机制

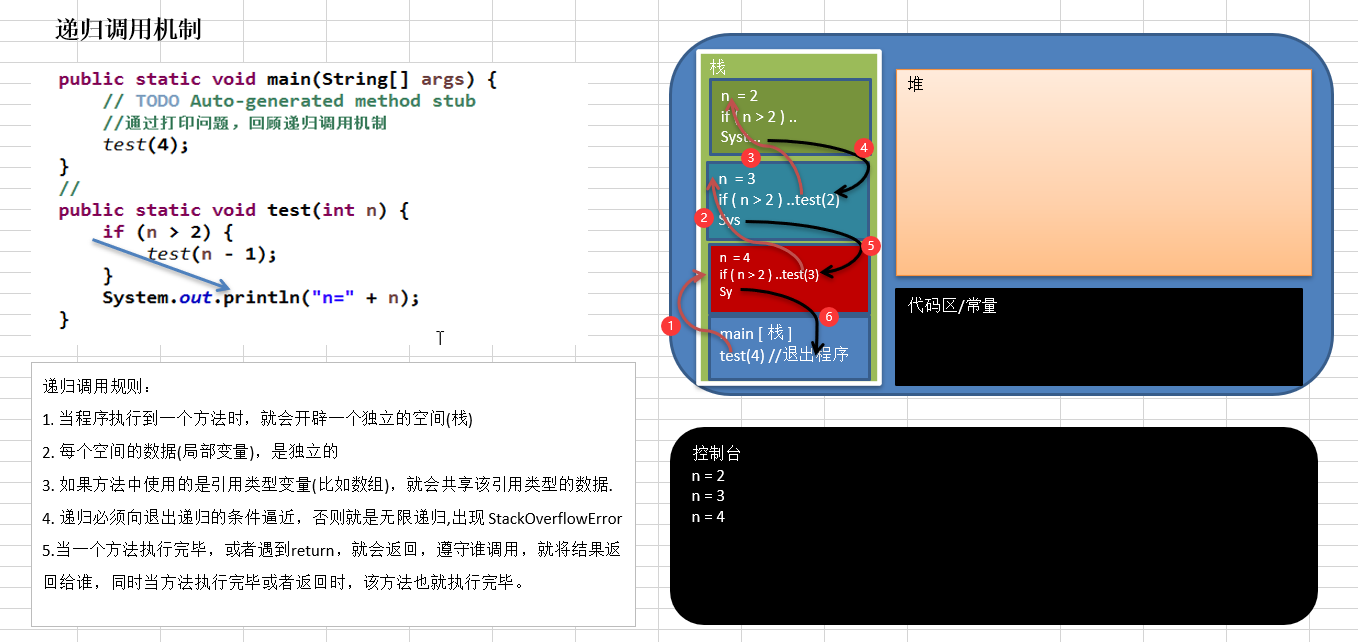
递归调用机制

递归调用规则

  • 执行一个方法时，就创建一个新的受保护的独立空间（栈空间）。

  • 方法的局部变量是独立的，不会相互影响, 比如 n 变量。

  • 如果方法中使用的是引用类型变量（比如数组），就会共享该引用类型的数据。

  • 递归必须向退出递归的条件逼近，否则就是无限递归,出现 StackOverflowError 错误，死龟了。

  • 当一个方法执行完毕，或者遇到 return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或者返回时，该方法也就执行完毕。

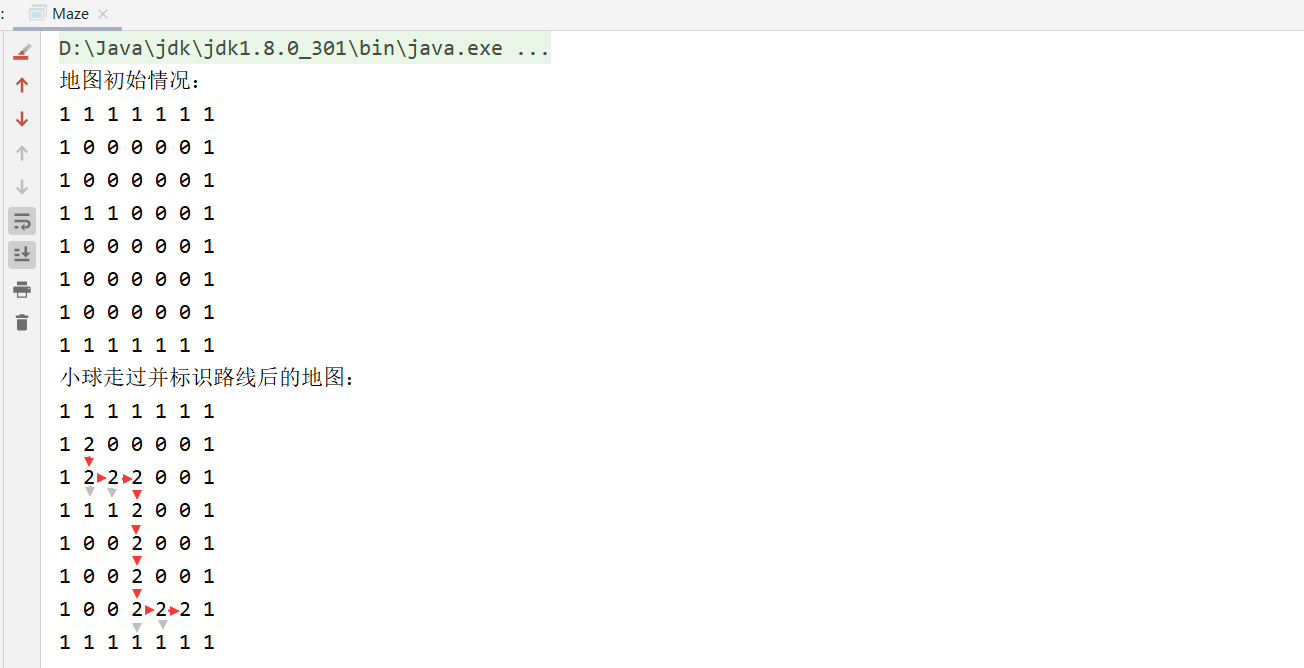
迷宫问题

思路分析

迷宫问题

两种策略

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
public class Maze {
    public static void main(String[] args) {
        // 先创建一个二维数组，模拟迷宫
        int[][] map = new int[8][7];
        // 使用 1 表示墙，最上最下两行全部置为 1
        for (int i = 0; i < 7; i++) {
            map[0][i] = 1;
            map[7][i] = 1;
        }

        // 最左最右两列全部置为1
        for (int i = 0; i < 8; i++) {
            map[i][0] = 1;
            map[i][6] = 1;
        }

        //设置挡板, 1 表示
        map[3][1] = 1;
        map[3][2] = 1;
        //map[1][2] = 1;
        //map[2][2] = 1;

        // 输出地图
        System.out.println("地图初始情况：");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }

        //使用递归回溯给小球找路
        setWay1(map, 1, 1);
        //setWay2(map, 1, 1);

        //输出新的地图, 小球走过，并标识过的递归
        System.out.println("小球走过并标识路线后的地图：");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }

    }

    /**
     * 使用递归回溯，按照策略 下->右->上->左  给找路
     * <p>
     * 约定：
     * 当map[i][j] 为 0， 表示该点没有走过 ；
     * 为 1 表示墙 ；
     * 为 2 表示通路可以走 ；
     * 为 3 表示该点已经走过，但是走不通；
     * 如果小球能到 map[6][5] 位置，则说明通路找到.
     *
     * @param map [in] 表示地图
     * @param i   [in] 开始位置横坐标
     * @param j   [in] 开始位置纵坐标
     * @return 如果找到通路，就返回true, 否则返回false
     */
    public static boolean setWay1(int[][] map, int i, int j) {
        // 通路已经找到
        if (map[6][5] == 2) {
            return true;
        } else {
            //如果当前这个点还没有走过
            //按照策略 下->右->上->左  走
            if (map[i][j] == 0) {
                // 假定该点是可以走通.
                map[i][j] = 2;
                if (setWay1(map, i + 1, j)) {//向下走
                    return true;
                } else if (setWay1(map, i, j + 1)) { //向右走
                    return true;
                } else if (setWay1(map, i - 1, j)) { //向上走
                    return true;
                } else if (setWay1(map, i, j - 1)) { //向左走
                    return true;
                } else {
                    //说明该点是走不通，是死路
                    map[i][j] = 3;
                    return false;
                }
            } else { // 如果map[i][j] != 0 , 可能是 1， 2， 3
                return false;
            }
        }
    }

    /**
     * 使用递归回溯，按照策略 上->右->下->左  给找路
     * 约定：
     * 当map[i][j] 为 0， 表示该点没有走过 ；
     * 为 1 表示墙 ；
     * 为 2 表示通路可以走 ；
     * 为 3 表示该点已经走过，但是走不通；
     * 如果小球能到 map[6][5] 位置，则说明通路找到.
     *
     * @param map [in] 表示地图
     * @param i   [in] 开始位置横坐标
     * @param j   [in] 开始位置纵坐标
     * @return 如果找到通路，就返回true, 否则返回false
     */
    public static boolean setWay2(int[][] map, int i, int j) {
        // 通路已经找到
        if (map[6][5] == 2) {
            return true;
        } else {
            //如果当前这个点还没有走过
            //按照策略 上->右->下->左
            if (map[i][j] == 0) {
                // 假定该点是可以走通.
                map[i][j] = 2;
                if (setWay2(map, i - 1, j)) { //向上走
                    return true;
                } else if (setWay2(map, i, j + 1)) { //向右走
                    return true;
                } else if (setWay2(map, i + 1, j)) { //向下
                    return true;
                } else if (setWay2(map, i, j - 1)) { // 向左走
                    return true;
                } else {
                    //说明该点是走不通，是死路
                    map[i][j] = 3;
                    return false;
                }
            } else { // 如果map[i][j] != 0 , 可能是 1， 2， 3
                return false;
            }
        }
    }

}

运行结果

八皇后问题

八皇后问题

思路分析

示例图

放置顺序

  1. 第一个皇后先放第一行第一列；

  2. 第二个皇后放在第二行第一列，然后判断是否OK。

    如果不OK，继续放在第二列、第三列…依次把所有列都放完，找到一个合适位置；

  3. 继续第三个皇后，还是第一列、第二列……直到第 8 个皇后也能放在一个不冲突的位置，算是找到了一个正确解；

  4. 当得到一个正确解时，在栈回退到上一个栈时，就会开始回溯，即将第一个皇后，放到第一列的所有正确解，全部得到；

  5. 然后回头继续第一个皇后放第二列，后面继续循环执行 1,2,3,4 的步骤 。

说明：理论上应该创建一个二维数组来表示棋盘，但是实际上可以通过算法，用一个一维数组即可解决问题。

arr[8] = {0 , 4, 7, 5, 2, 6, 1, 3}

arr 下标表示第几行，即第几个皇后;

arr[i] 的值表示皇后在该行的位置。

arr[i] = val ：表示第 i+1 个皇后，放在第 i+1行 的第 val+1列。

位置判断

  • array[i] == array[n]

    表示判断第 n 个皇后是否和前面的 n-1个皇后在同一列

  • Math.abs(n-i) == Math.abs(array[n] - array[i])

    表示判断第 n 个皇后是否和第 i 个皇后在同一斜线上。

    如第二个皇后放 n=1位置，即二行二列位置，此时：n=1， array[1] = 1：

    1
    2
    Math.abs(1-0) == 1
    Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1

    此时该位置在同一斜线上，所以不合适。

    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
    0 1 2 3 4 5 6 7
  1. 没有必要判断是否在同一行，因为摆放时 n 每次都在递增

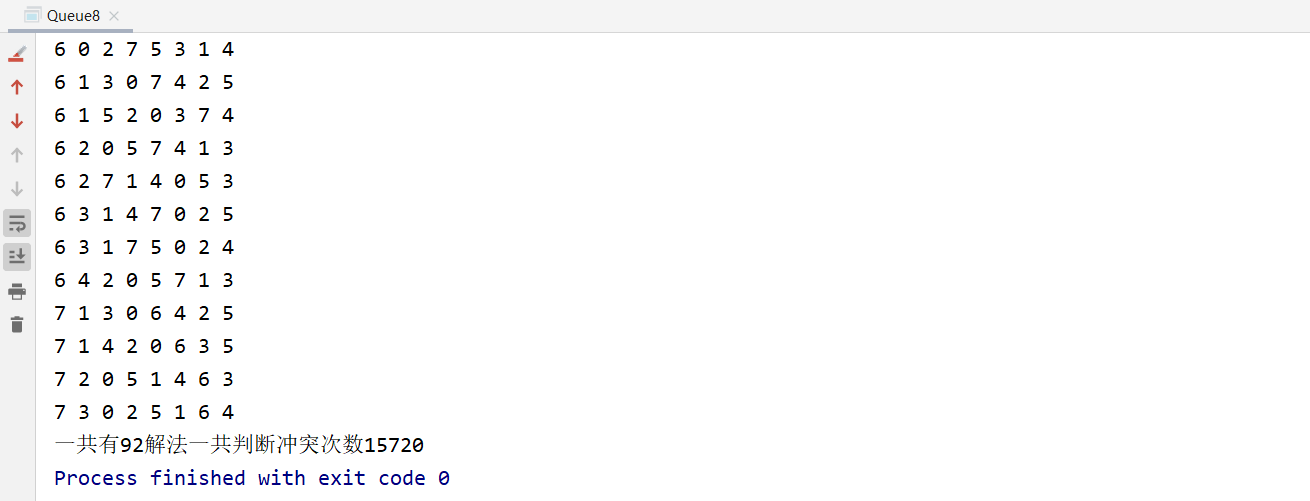
代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public class Queue8 {


    /**
     * 表示共有多少个皇后
     */
    int max = 8;
    /**
     * 数组array, 保存所有皇后最终放置位置,比如 arr = {0 , 4, 7, 5, 2, 6, 1, 3}
     */
    int[] array = new int[max];
    static int count = 0;
    static int judgeCount = 0;

    public static void main(String[] args) {
        //测试一把 ， 8皇后是否正确
        Queue8 queue8 = new Queue8();
        queue8.check(0);
        System.out.printf("一共有%d解法", count);
        System.out.printf("一共判断冲突次数"+ judgeCount);

    }

    /**
     * 放置第 n+1 个皇后
     * 特别注意：每一次递归时，进入到 check 中都有 for(int i = 0; i < max; i++)，因此会有回溯
     *
     * @param n [in]
     */
    private void check(int n) {
        //n = 8 , 其实8个皇后已经放好
        if (n == max) {
            print();
            return;
        }
        //依次放入皇后，并判断是否冲突
        for (int i = 0; i < max; i++) {
            //先把当前这个皇后n （第 n=1 个皇后）, 放到该行的第 1 列
            array[n] = i;
            //判断当放置 皇后n 到 i 列时，是否冲突
            if (judge(n)) {
                //不冲突，接着放 皇后n+1,即开始递归
                check(n + 1);
            }
            //如果冲突，就继续执行 array[n] = i; 即将皇后n，放置在本行后移一个位置
        }
    }

    /**
     * 检测当前放置的皇后是否和前面摆放的皇后冲突
     *
     * @param n [in] 表示第 n 个皇后
     * @return
     */
    private boolean judge(int n) {
        judgeCount++;
        for (int i = 0; i < n; i++) {
            // 说明
            // 1. array[i] == array[n]
            //        表示判断第 n 个皇后是否和前面的 n-1个皇后在同一列
            // 2. Math.abs(n-i) == Math.abs(array[n] - array[i])
            //        表示判断第 n 个皇后是否和第 i 个皇后是否在同一斜线
            //        如第二个皇后放 n=1位置，即二行二列位置，此时 n=1， array[1] = 1
            //        Math.abs(1-0) == 1
            //        Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
            //3. 没有必要判断是否在同一行，因为摆放时 n 每次都在递增
            if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
                return false;
            }
        }
        return true;
    }

    /**
     * 将皇后摆放的位置输出
     */
    private void print() {
        count++;
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }

}

运行结果